どうも、いちにょきです(^^)/
機械科目に照明計算がありますが、みなさんはどのように解いているでしょうか?
照明計算については普通は馴染みがなく、電験で初めて触れたというかたが多いと思います。
そして馴染みがないので、他の科目に比べて捨てられがち(あまり勉強されない)な分野でもあります。正直私も最初は、馴染みのない照明を0から勉強するより、他の分野の勉強に力を入れたほうがいいのでは?と思っていました。
しかし、勉強を少ししてみて、「あれ、これ意外と簡単じゃね?」と思い直し、真面目に勉強して、得点源にしました。
そこで今回は、照明計算を勉強するときのポイントを解説いたします。
照明計算に必要な公式と各公式のポイント
照明計算では覚えておかないといけない公式がいくつかあります。
そして、照明計算の出来はこの公式の理解でほぼ決まると言っても過言ではありません。そして逆説的に、これらの公式をしっかりと理解できていれば、あとは幾何的な概念(ベクトル、立体角、三角形など)とこれらの公式のいくつかを組み合わせることで解ける問題ばかりです。
以下ではそれらの公式を列挙しながら、ポイントを解説していきます。基本的な事項や詳しい説明はお持ちの参考書に譲ろうと思います。プラスアルファの知識として読んでみてください。
また、照明分野の公式を覚える際は、単位もセットで覚えることが大事です!
単位を見ることでその物理量が何を表しているのかがわかるからです。
それでは行きましょう!
立体角\(\omega\)
\(\omega = \frac{S}{r^2}\) [str]
2次元の角度を3次元に拡張した概念で、単位は[str]で表されます。
空間の広がりを表す量で、面積を起点からの距離の2乗で割った値です。
球の立体角は\(\omega = 4 \pi\)となります。
光度\(I\)と光束\(F\)
\(I = \frac{F}{\omega}\) [cd] = [lm/str]
ただし、光束 \(F = \omega I\) [lm]
上の二式は同じもので、変形しただけですね。式としては片方覚えておけばよいです。
光束\(F\)の単位は[lm]で表されます。
光度\(I\)は単位立体角当たりの光束\(F\)なので、単位としては
[cd] = [lm/str]
です。
照度\(E\)
\(E = \frac{F}{S}\) [lx] = [lm/\({\rm m}^2\)]
照度は被照面(照らされる面)に注目した量で、単位面積当たりの入射光束を表しています。したがって単位としては
[lx] = [lm/\({\rm m}^2\)]
となります。
輝度\(L\)
\(L = \frac{I}{S'}\) [cd/\({\rm m}^2\)]
ただし、\(S'\): 見かけの面積
光源のある方向の輝度は、その方向の光度をその方向の見かけの面積で割った値で定義されています。少しわかりにくいですね。
例えば球の発光源の場合は、その球を見たときに見える円の面積が見かけの面積で、その円を通過する光度を見かけの面積で割ることで求められます。
単位は[cd/\({\rm m}^2\)]です。
光束発散度\(M\)
\(M = \frac{F}{S}\) [lm/\({\rm m}^2\)]
光束発散度は光源に注目した量で、ある面から発散する光束をその面の表面積で割った値です。
単位は[lm/\({\rm m}^2\)]で、照度と同じです。照度は照らされる側(被照面)の量、光束発散度は照らす側(光源)の量という違いがあります。
また、完全拡散面では\(M = \pi L\)が成り立ちます。
この式はわかりにくいと思うので少し解説します。
まず完全拡散面とは、輝度が方向によらず一定となる(どの方向から見ても輝度が同じ)面のことです。
ここで下図のような完全拡散面の球光源を考えてみます。(手書きで申し訳ないです(^^; )
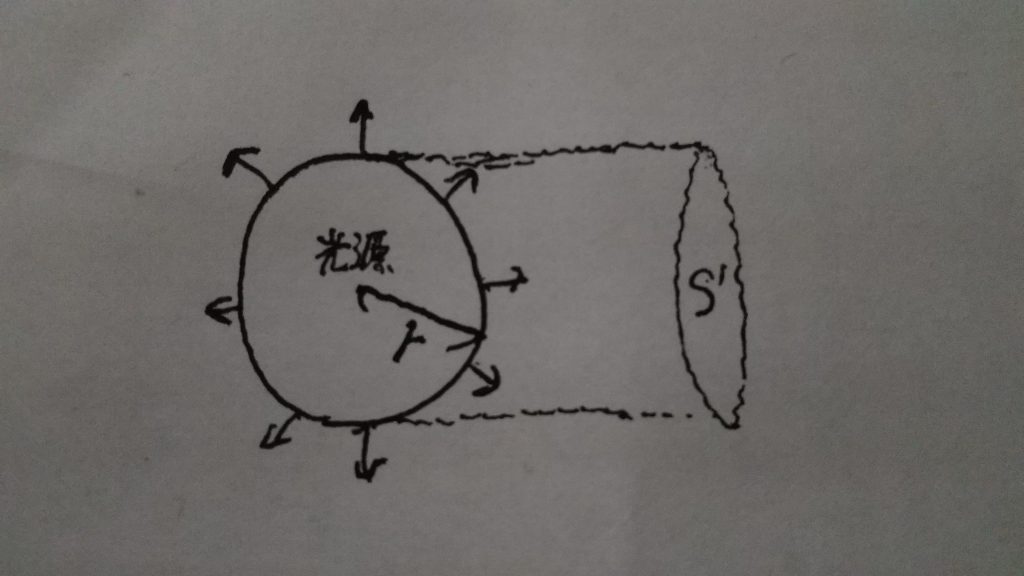
輝度の公式から
\(L = \frac{I}{S'}\)
です。図から\(S' = \pi r^2\)ですね。
また光度\(I\)の公式を立体角の定義式を使って変形すると、
\(I = \frac{F}{\omega} = \frac{r^2 F}{S} = \frac{r^2 F}{4 \pi r^2} = \frac{F}{4 \pi}\)
となり、これを使って輝度\(L\)を変形すると、
\(L = \frac{I}{S'} = \frac{F}{4\pi S'} = \frac{F}{4\pi^2 r^2}\)
となりますね。よって
\(\pi L = \frac{F}{4\pi r^2} = \frac{F}{S} = M\)
となって\(M = \pi L\)が導けました。今回はイメージしやすいように球光源を用いましたが、完全拡散面という条件を満たしていれば\(M = \pi L\)は成り立ちます。
\(M = \pi L\)の関係を思い出せなくなったら、球光源を思い出すとよいでしょう。
照明率と保守率
これら二つは物理量ではなく、性能を評価する指標や係数のようなものなのですが、知っている前提で問題に出てくるので覚えましょう。
照明率は光源の光束に対して実際に照らしたい面にどれくらいの光束が届いたかを評価する指標で、
照明率 = 実際に届く光束/光源の光束
で表されます。
保守率は被照面の照度の、時間による減衰係数です。例えば被照面に必要な照度があり、その照度を確保するためにどれだけの光源を用意すればよいかを計算したとします。
しかし、実際には時間の経過とともに光源の光束は減衰し(新品の電球のほうが明るいですよね!)、被照面の照度も減衰します。
つまり実際にはその減衰を考慮して光源を設置しなければならないので、保守率のような補正係数をもちいる必要が出てくるわけです。よって、大抵数値で与えられて計算に用いることが多いです。式で書くと、
保守率 = 照明器具設置時の被照面照度/被照面の確保すべき照度
となります。
例題
平成30年度電験3種・機械・問17の問題です。

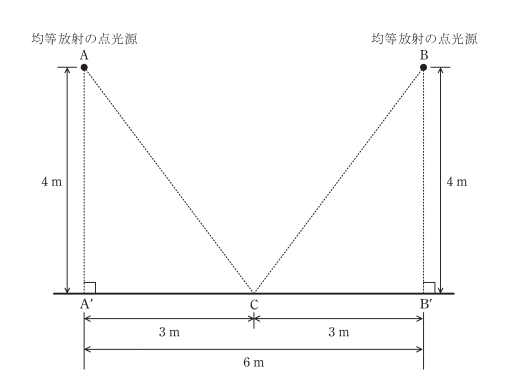
解答
「どの方向にも光度が等しい均等放射の点光源」とあるので、完全拡散面ですね。
(a)A'の水平面照度(面に対して垂直方向の照度)を問われています。照度の式は\(E = \frac{F}{S}\) [lx]ですから、光束\(F\)と面積\(S\)がわかれば出せます。
点光源の全光束は15000lmと与えられているので、点光源を中心とした半径4mの球を考えれば、
\(E = 15000/4 \pi 4^2 = 74.6\) → 75lx
(b)まずAが作るCでの照度の、水平面方向成分を求めます。
AC間の距離は三平方の定理から5となるので、(a)のときと同様に半径5の球を考えれば、
\(E = 15000/4 \pi 5^2 = 47.75\)
角CAA'を\(\theta\)とすると、\(\cos \theta = 4/5\)となるので、水平面照度\(E_n\)は
\(E_n = E\cos \theta = 38.20\)
点光源が二つあるので
\(38.20 \times 2 = 76.40\) → 76lx
となります。
この問題は照明の中でも比較的簡単な部類ではありますが、基本的にはこのように照明の物理量にかかわる公式、幾何的な概念(ベクトル、立体角、三角形など)が理解できていれば、さほど難しい問題は出ません。いくつか問題を解いてパターンがわかれば得点源になります。
照明分野の計算のコツ(まとめ)
今回は照明分野の計算のコツについて解説しました。ポイントをまとめます。
- 紹介したポイントを押さえながら公式を覚えよう。
- 公式と幾何的な概念(ベクトル、立体角、三角形など)が理解できていれば、照明分野はさほど難しくない。
個人的には、照明分野を捨てるのはかなりもったいないと考えます。照明自体は0から勉強するとしても、費用対効果の高い分野ですので、勉強することをおすすめします。
