どうも、いちにょきです!
みなさん水頭って理解していますか?
私も勉強を始めたときに、水の頭???なにそれおいしいの???となった覚えがあります笑
今回はこの水頭と、関連の深いベルヌーイの定理について解説していきます。
ベルヌーイの定理
「いや、水頭の説明をしろww」
なんて声が聞こえてきそうですが、ベルヌーイの定理からスタートすることが重要なポイントなのです笑
さて、ベルヌーイの定理は完全流体(※)という仮定のもとで成り立つ、流体のエネルギー保存式です。
完全流体とは粘性(流体の粘り気、とろみのようなもの)がなく、圧縮できない(体積変化がない)と仮定した理想的な流体のこと。
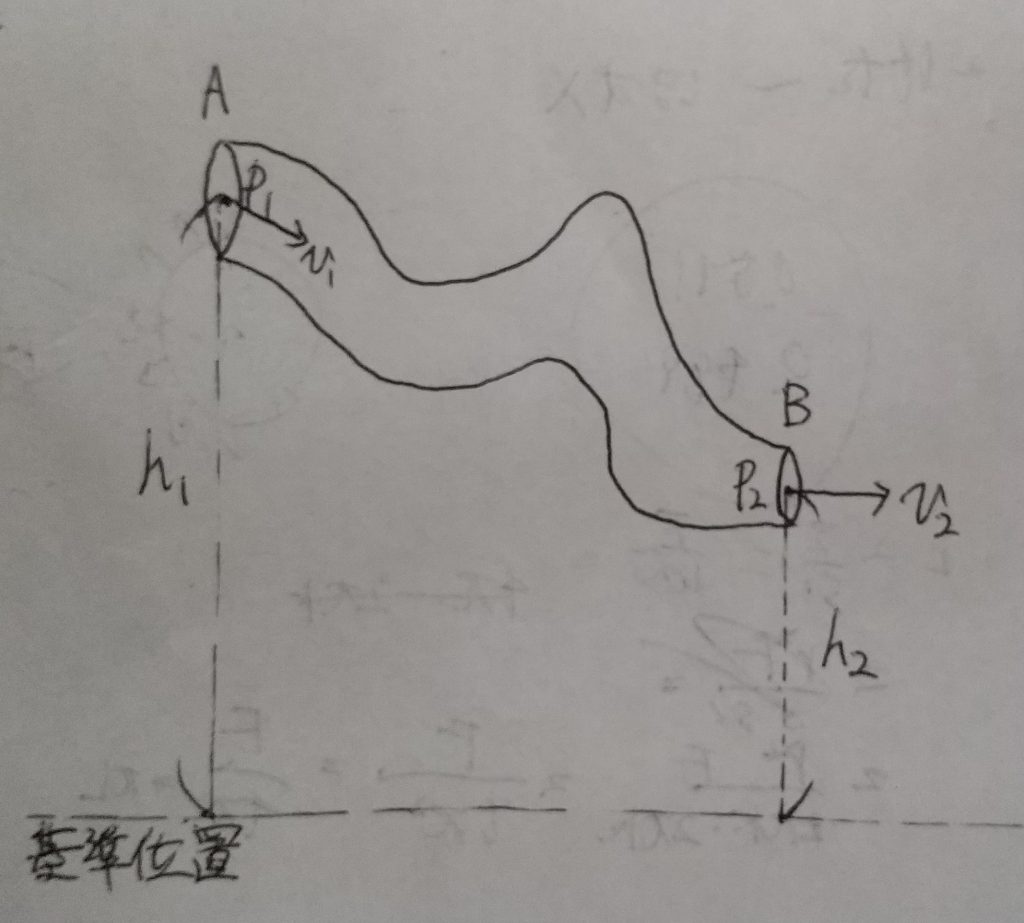
上図のような管を流れる完全流体を考えた場合、以下のエネルギー保存則が成り立ちます。
\(mgh_1 + m\frac{p_1}{\rho} + \frac{1}{2}m{v_1}^2 = mgh_2 + m\frac{p_2}{\rho} + \frac{1}{2}m{v_2}^2\)
ただし\(m\)は単位時間あたりに管を流れる流体の質量(質量流量)です。今圧縮のない流体を考えているので、管のどこでも\(m\)は一定ですね。
\(g\)は重力加速度、\(\rho\)は流体の密度、\(h\)は位置、\(v\)は速度です。
この式をベルヌーイの定理といいます(式変形によって形は色々ある)。
両辺の第一項\(mgh\)が位置のエネルギー、第二項\(m\frac{p}{\rho}\)が圧力のエネルギー、第三項\(\frac{1}{2}m{v}^2\)が運動のエネルギーです。ベルヌーイの定理を言葉で書けば、
位置エネルギー + 圧力エネルギー + 運動エネルギー = 一定
となります。
ところで、中学生くらい(?)のときに、力学的エネルギー保存の法則って出てきませんでした?
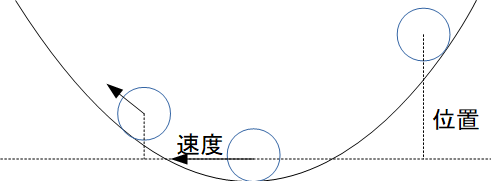
位置エネルギー + 運動エネルギー = 一定
というやつです。物体の運動について力学的エネルギー保存則を考えたように、流体にも適用したものがベルヌーイの定理です。
力学的エネルギー保存則もベルヌーイの定理も、エネルギー保存はどの位置でも成り立っているため、途中の経路は関係ありません。図1の管をわざといびつな形にしているのはこれを示すためです。決して絵が下手なわけではありません。
水頭とは
準備が整ったところでお待ちかね(?)水頭の説明をします
さきほどのベルヌーイの定理を両辺を\(mg\)で割ると、
\(h_1 + \frac{p_1}{\rho g} + \frac{1}{2g}{v_1}^2 = h_2 + \frac{p_2}{\rho g} + \frac{1}{2g}{v_2}^2\)
となります。この式の単位(次元)は\(h_1\)や\(h_2\)がそのまま含まれていることからわかるように[m]ですね。
このとき圧力エネルギーは\(\frac{p}{\rho g}\)、運動エネルギーは\(\frac{1}{2g}{v}^2\)となります。
この\(\frac{p}{\rho g}\)を圧力水頭、\(\frac{1}{2g}{v}^2\)速度水頭と呼びます。
つまりベルヌーイの定理で位置(高さ)の次元にそろえた圧力エネルギーと運動エネルギーのことをそれぞれ圧力水頭、速度水頭と言っているわけです。位置はそのまま位置水頭です。
エネルギー保存則を位置の次元にそろえて、位置、圧力、速度のエネルギーのやり取りを、位置、圧力、速度の水頭のやり取りとして考えようぜ!というのが水頭の考え方なのです。
参考書などでいきなり「圧力水頭とは\(\frac{p}{\rho g}\)である!」なんて出てくるから、「いや、ちょっと待てどこから出てきたww」ってなるんです。私がそうでした笑
でもベルヌーイの定理から考えれば理解しやすいですね。
水頭とベルヌーイの定理について(まとめ)
今回は水頭とベルヌーイの定理について解説しました。ポイントをまとめます。
- 力学的エネルギー保存則を考えたように、流体にもエネルギー保存則を適用したものがベルヌーイの定理
- 水頭とはベルヌーイの定理を位置の次元にそろえて、位置、圧力、速度のエネルギーのやり取りを、位置、圧力、速度の水頭のやり取りとして考えたもの
では引き続き勉強がんばってくださいね(^^)/
