いちにょきです!
さて、今回は電験3種の火力発電所に関わる計算とその周辺の用語解説を行おうと思います!
なぜかというとこの単元、簡単で得点源になるからです笑
もし、得意意識のない方がいらっしゃいましたら、ぜひこの記事を読んで得意分野にしてくださいね!
用語解説
計算を始める前に、用語の定義やポイントを解説しておきましょう。
エンタルピー
熱力学を学んだことのある方なら説明は不要だと思いますので、ここでは熱力学を学んだことのない方向けに簡単にイメージを説明します。
エンタルピーは物質(ここでは気体としましょう)のエネルギー状態を表すのに使われる概念です。
気体の加熱・冷却、気体の圧縮・膨張(外部との仕事のやり取り)といったような影響で増減します。
エンタルピーがよくわからない方はとりあえず「物質が持っているエネルギーを数値化したもの」と考えておいてください。
蒸気の性質
水を加熱し続けたときの変化について考えてみましょう。
下の図は水を加熱し続けたときの水の温度とエントロピーを表しています。
エントロピーについては電験3種では詳しく取り上げられることはないので、とりあえずそんな量があるのだなあくらいに考えておいてください(気になる人は自分で調べてみてくださいね。)。
水を加熱すると横軸のエントロピーは増加していきます。
はじめは加熱に伴い温度を上げていきます。この段階は図の①にあたります。
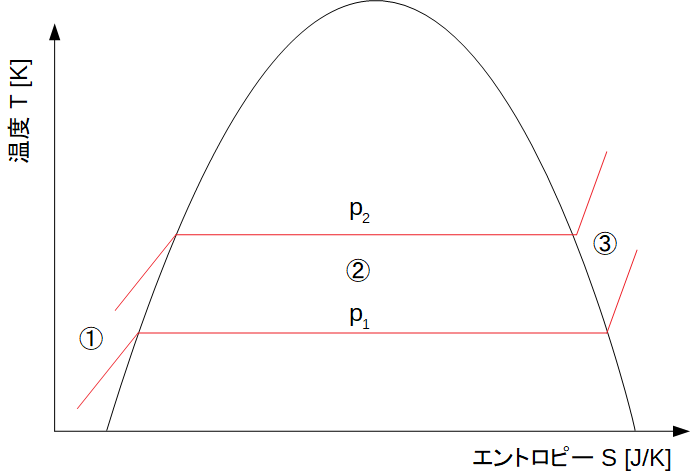
そしてある温度に到達すると、加熱しても温度が上昇しなくなります。
この段階は図の②にあたります。温度が上昇しなくなっているのがわかりますね。
ここでは水と蒸気が共存した状態です。
ちなみに温度上昇しなくなる時の温度は圧力によって変化しますが、我々が生活している大気圧では100℃(373K)です。
さて、温度上昇しなくなった水をさらに過熱し続けると、水はすべて蒸気となり、加熱に伴ってさらに温度を上げていきます。
図の③にあたります。
水の加熱は上記のように進行します。
③の状態にある蒸気を乾き飽和蒸気と言います。
②の状態は完全に蒸気になれていない微細な水滴と乾き飽和蒸気が含まれており、湿り蒸気と言います。
湿り蒸気1[kg]中にx[kg]の乾き飽和蒸気が含まれ、残りの1-x[kg]が微細な水滴である場合、xを乾き度、1-xを湿り度と言います。
感覚的に説明すると湿り度とは、②の蒸気は完全な蒸気と、微細な液体の水が共存しているため、それを「蒸気がどれだけ湿っているのか」と表現し、数値化したものです。
熱効率
熱効率 = (発生した電力量[kJ]/消費した燃料の熱量[kJ]) × 100 [%]
で表されます。消費した燃料の熱量からどれだけ電気を取り出せたかを表しています。シンプルですね。
熱消費率
「1[kW-h]を発生させるのにどれだけの熱量[kJ]を消費したか」を示すもので、「消費した熱量[kJ]÷発生した電力量[kW-h]」で表されます。
ここで熱消費率と熱効率の関係について説明しておきます。
実は、熱効率を\(\eta\)[%]とすると、
\(H = \frac{3600}{\eta} \times 100 \) [kJ/kW-h]
で表されます。なぜこうなるかというと、
まず熱消費率は「消費した熱量[kJ]÷発生した電力量[kW-h]」でしたね。
これはまさに熱効率と分母分子が逆の関係になっています。
熱効率[%]の逆数を考えると、「消費した熱量÷発生した電力量 [1/%]」なので、まず[1/%]を×100として数値に戻してやります。
次に分母分子に[kJ]をかけ、分母の[kJ]を[kW-h]に直すために分子に3600をかければ熱消費率の式となります。
\(H = \frac{3600}{\eta} \times 100 \) [kJ/kW-h]
発電端と送電端
発電所で発電された電力は送電線にて送電されるのですが、全量が送電されるわけではありません。
どういうことかというと、発電所の補機(コンプレッサーやポンプなど)を動かすのに必要な所内電力が発電した電力から差し引かれるからです。
この所内電力量を引く前(すなわち発電機の末端)のポイントを発電端、所内電力量を引いた後(すなわち送電線の送る側の端)のポイントを送電端といいます。
図で表すとこうなります。

ちなみに送電分野では受電端という言葉が出てきますが、これは需要家(送電線の末端)のポイントを指します。
設備利用率
設備利用率 = 発生電力量/認可出力 × 運転時間
です。例えば一日の設備利用率がわかれば、認可出力(その発電機が出せる最大の出力)で24時間発電した場合と比べて、どれくらいの電力を発電したかがわかります。
ポイント
熱計算関係の問題でポイントとなるのは、上記のような用語の定義を理解しておくことと、単位の変換をミスなくできるようになることです。
単位の変換についてはこちらの記事で解説しています。
-

電験・エネ管受験者のための単位の考え方&計算方法[電験3~1種・エネ管合格者が解説]
どうも、いちにょきです! 今回は単位換算の方法や考え方について解説していきます。単位換算が自由にできると解ける問題の幅が増えます。 また単位についての考え方も解説していますので、これを読めば計算ミスを ...
続きを見る
例題
ここでは例題として令和元年度第3種電気主任技術者試験電力科目の問15を解いてみたいと思います。

(a)熱消費率[kJ/(kWh)]は「消費した熱量[kJ]÷得られた電力量[kWh]」で求められましたね。
得られた電力量がわからないのでx[MW]とします。熱消費率はわかっているので、あとは消費した熱量がわかれば解けますね。
消費した熱量は電力と損失のふたつに形を変えているので、得られた電力量x[MW]と損失(冷却水が持ち去る熱量)の単位をそろえて足すことで表すことができます。
したがって1h分の熱量を考えると、
8000[kJ/(kWh)]
= (103x × 3600 + 3.1×109) [kJ] / 103x [kWh]
という式が出来上がります。あとはこれを解いてやれば、
x \(\simeq\) 700 [MW]
となります。
(b)冷却水の温度上昇を\(\Delta\)とします。
1秒間に通水する冷却水に対して、持ち去られる熱量[kJ/s]と温度上昇に使われる熱量[kJ/s]が等しいので、そこから方程式を作ればよいですね。
1秒間に通水する冷却水の質量は、
30 [m3/s] × 1.1 × 103 [kg/m3]
= 3.3 × 104 [kg/s]
なので、単位を[kJ/s]にそろえて
3.3 × 104 [kg/s] × 4.0 [kJ/(kg-K)] × \(\Delta\) [K]
= 3.1 × 109/3600 [kJ/s]
という方程式が立式できます。
これを解いて、
\(\Delta \simeq 6.5\) [K]
となります。
火力発電所の熱計算における用語・ポイント(まとめ)
今回は熱計算周りの用語解説と例題演習を行いました。
熱計算は基本的な用語の定義と単位換算ができれば、方程式を作って簡単に解けることがわかったと思います。
この分野はかなり得点源になるので、確実にものにしていきましょう!

